Analysis of the Rubik Cube Dance

by Peter Foster

Home | Dance Home

Last modified 7 April 2006

This is an analysis of the transformations in the Rubik Cube dance. Comments are welcome - email pfoster@pcug.org.au

The dance is for nine people in a 3x3 square, as follows:

		Back
Left				Right
		Front

This is the view from the front (the caller's view). Note that real life dancers are a lot sharper than the ones shown here...

There are only three types of move in the dance, as follows:

1. One side passes through to the other side
2. The eight outside people circle halfway around
3. A reel of three, in each line or column (this does not change anyone around, it is a "nothing" move)

By doing these moves in various combinations it is possible to reach any of 18 possible arrangements. These are shown in the following diagrams (the arrows show where each person moves to, for example diagram G shows the result of the front line passing through).

C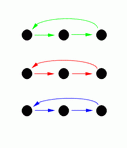	D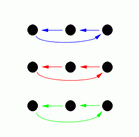	G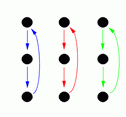	H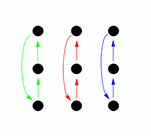
J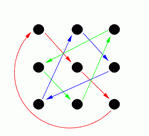	K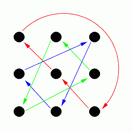	P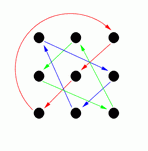	Q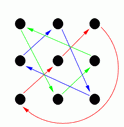
I			M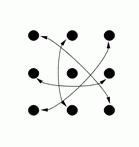
T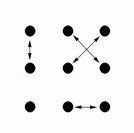	V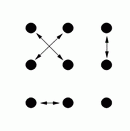	W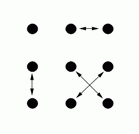	Y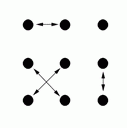
F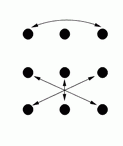	B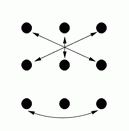	R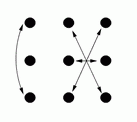	L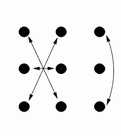

Diagrams C, D, G and H show the result of one side passing through to the other side, and diagram M shows the result of a circle halfway (and diagram I shows the result of a reel of three).

Note that there are two categories of arrangements:

1. Some (those with the coloured arrows) have everyone moving to a new position, in three cycles of three people each (each three person cycle is shown in a different colour to make them slightly clearer). Since each person is moving in a cycle with three people, if you do one of these three times in a row you will finish with everyone back where they started. Because of this, we will call these arrangements "Type 3".
2. The other arrangements (those with the black arrows) leave one person unmoved and swap the others in pairs. Since people are swapped in pairs, doing the same one again will put everyone back where they started. We will call these "Type 2".

Now let's look at what happens when you combine various types of arrangements.

If you do two of the same type in a row (i.e. type 2 followed by a type 2, or a type 3 followed by a type 3) then you will finish in a type 3. If you do two different types in a row (i.e. type 2 followed by a type 3, or a type 3 followed by a type 2) then you will finish in a type 2. For example, T (type 2) followed by D (type 3) results in B (type 2).

In this dance, the "turn one side" move (circle halfway, then one side passes through) corresponds to M followed by C, D, G or H. This results in R, L, F and B respectively, which are all type 2. In the dance we do three of these. When you do three type 2's in a row, you finish with a type 2 (this is easily seen: two type 2's in a row will result in a type 3, doing another type 2 results in a type 2).

Since the result of the three "turn one side" moves is a type 2, repeating it will get everyone back where they started. This is why the dance works as it does: doing the same three moves in the same order simply swaps everyone back to where they started.

(I should also mention that the initial part of the dance, where each side in turn passes through, leaves the order unchanged.)

The Four Turn Version

The "advanced" version, with four turn-one-side moves, is more complicated. This is structured as follows:

• The initial bit (each side passes through)
• The four turn-one-side moves
• The last bit, which has the same effect as a circle halfway

The four turn-one-side moves (type 2) in a row result in a type 3, which is a bit harder to restore. We could restore by doing the moves in reverse order, but that's too difficult for the dancers (or caller, for that matter) to remember. What I did is to add on that last bit, which has the effect of a type 2 move. This makes total of 5 type 2's in a row, which results in a type 2, so repeating the moves will get everyone back to where they started.

Results of Various Move Combinations

Finally, here is a table showing the results of various two move combinations (for example, B followed by F results in H). I haven't included all second moves, only those that are related to the dance moves.